Omar Khayyam-Mathematician, Astronomer, And Poet

In the year 1072 AD, Omar Khayyam documented the most accurate year length ever calculated – a figure still accurate enough for most purpo...

In the year 1072 AD, Omar Khayyam documented the most accurate year length ever calculated – a figure still accurate enough for most purposes in the modern world. Khayyam was an astronomer, astrologer, physician, philosopher, and mathematician: he made outstanding contributions in algebra. His poetry is better known in the West than any other non-Western poet.

The man himself remains something of an enigma. Different biographers have documented him as a fun-loving, wine-drinking agnostic; a closet Zoroastrian; a Sufi Muslim; an orthodox Sunni Moslem; and a follower of Ancient Greek philosophy. All agree that he was an outstanding intellectual.

Lived 1048 – 1131.

Beginnings

Omar Khayyam was born on May 18, 1048 in the great trading city of Nishapur in northern Persia. Today the city is in Iran. Omar’s father was Ebrahim Khayyami, a wealthy physician. Omar’s mother’s name is not known. Some authors have written that Omar’s father earned a living making tents, because Khayyami means tent-maker. However, although many English-speakers are named Smith, it does not mean their fathers spent their days hammering hot metal on an anvil.

Omar’s family were Muslims. His father seems to have been relaxed about religion, employing a mathematician by the name of Bahmanyar bin Marzban, a devotee of the ancient Persian religion of Zoroastrianism, to tutor Omar. Bahmanyar had been a student of the great physician, scientist, and philosopher Avicenna, and he gave Omar a thorough education in science, philosophy, and mathematics. Khawjah al-Anbari taught Omar astronomy, guiding him through Ptolemy’s Almagest.

In his early teens Omar worked in his father’s surgery learning about medicine.

Omar Khayyam celebrated his eighteenth birthday in 1066. In the same year, Halley’s comet appeared in the heavens, William the Conqueror’s Norman Army invaded England, and Omar’s father Ebrahim died. A few months after Ebrahim’s death, Omar’s tutor Bahmanyar also died.

It was the end of an era in Omar Khayyam’s life. It was time to put his family’s affairs in order and move on.

Samarkand

Omar Khayyam joined one of the regular caravans making a three month journey from Nishapur to the great city of Samarkand, which is now in Uzbekistan. Samarkand was a center of scholarship, and Khayyam arrived there probably in 1068, aged 20.

In Samarkand he made contact with his father’s old friend Abu Tahir, who was governor and chief judge of the city. Tahir, observing Khayyam’s extraordinary talent with numbers, gave him a job in his office. Soon Khayyam was given a job in the king’s treasury.

While living in Samarkand, Khayyam made a major advance in algebra.

Omar Khayyam’s Contributions to Science

Algebra

At high school, we learn about equations of the form ax2 + bx + c = 0; these are called quadratic equations. Cubic equations are of the form ax3 + bx2 + cx + d = 0. Naturally, cubic equations are harder to solve than quadratics.

Khayyam conjectured correctly that it is not possible to solve cubic equations using the traditional Ancient Greek geometrical tools of straightedge and compass. Other methods are required.

At the age of 22, in 1070, Khayyam published one of his greatest works: Treatise on Demonstration of Problems of Algebra and Balancing. In it he showed that a cubic equation can have more than one solution. He also showed how the intersections of conic sections such as parabolas and circles can be utilized to yield geometric solutions of cubic equations. Archimedes had actually started work in this field over a thousand years earlier, when he considered the specific problem of finding the ratio of the volume of one part of a sphere to another. Khayyam considered the problem in a more general, methodical way.

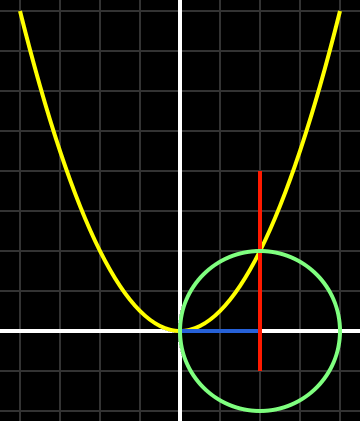
In the language of modern mathematics, Khayyam’s solution to the equation x3 + a2x = b features a parabola of equation x2 = ay, a circle with diameter b/a2, and a vertical line through the intersection point. The solution is given by the distance on the x-axis between the origin and the (red) vertical line. Image by Pieter Kuiper.

Khayyam’s solutions avoided negative coefficients and negative roots because negative numbers were not acknowledged in Islamic mathematics. (Some cultures, however, had incorporated negative numbers into mathematics – for example Brahmagupta had introduced negative numbers into Indian mathematics 400 years earlier.)

Although Khayyam’s achievement was magnificent, he was personally disappointed that he needed to utilize geometry to solve cubic equations – he had hoped to discover an algorithm using only algebra.

Treatise on Demonstration of Problems of Algebra and Balancing established Khayyam as a mathematician of the first rank, and his reputation spread quickly throughout Persia.

Following Khayyam’s breakthrough there was little significant progress on cubic equations until 1535, when Niccolo Tartaglia found general solutions for all cubic equations.

Khayyam’s algebra was not the system of letters and signs we use today. His algebra was expressed in words. So, where today we write:

Solve for x:

x2 + 6 = 5x

Khayyam wrote: What is the amount of a square so that when 6 dirhams are added to it, it becomes equal to five roots of that square?

Linking Algebra and Geometry

Algebra and Geometry were successfully linked by Pierre de Fermat and René Descartes in the 1600s, resulting in the modern x-y coordinate system.

Khayyam’s work with cubics had made him certain that algebra and geometry were linked, and he cited Euclid’s Elements to support the idea:

Length of Year

In 1073, Khayyam received an invitation to the Persian city of Isfahan, capital of the Seljuk Empire, to prepare a calendar that would work in an orderly way and be accurate forever – this was an era in which year lengths were regularly changed.

Khayyam’s invitation came from the two most powerful men in the Seljuk Empire, of which Persia was part: these were Malik Shah, Sultan of the Great Seljuq Empire, and Nizam al-Mulk, his vizier.

Khayyam recruited other talented scientists to accompany him to Isfahan in 1074. There he was paid an extraordinarily high salary and enjoyed a privileged lifestyle. Malik Shah paid Khayyam to found an observatory with an initial aim of making observations of the heavens for 30 years, during which time Saturn, the most distant planet then known, would complete an orbit.

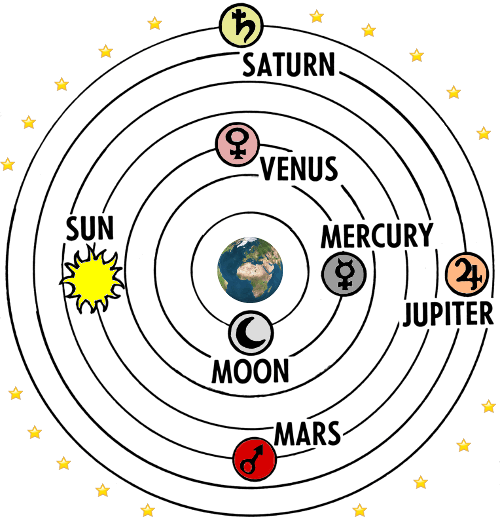
Ptolemy’s universe – the model accepted by Omar Khayyam.

During his time in Isfahan, Khayyam measured the length of a year – to be specific the tropical year length – with remarkable accuracy and precision.

Khayyam found that 1,029,983 days made 2,820 years. This gives a tropical year length of 365.2422 days to seven significant figures. Although it has become fashionable to quote more decimal places than this, Khayyam’s input of 1,029,983 days contains seven significant figures, so it is unreasonable to quote more than this number of significant figures in the calculated year length.

Today we know that the length of a tropical year actually changes by as much as 30 minutes from year to year. The average tropical year length quoted today is 365.242189 days, which to seven significant figures is 365.2422 days – exactly the figure Khayyam arrived at almost a thousand years ago. The length of a tropical year is also increasing very slightly as time passes, although not enough between Khayyam’s era and our own to be noticeable on a scale of seven significant figures.

Malik Shah introduced Khayyam’s new calendar in the Seljuk Empire on March 15, 1079. It was used until the 20th century.

The Parallel Postulate

The 13 books of Euclid’s Elements published in about 300 BC were probably the most influential books in the entire history of mathematics. The Elements had been built on five geometric postulates – in other words five things that were assumed to be true about geometry: for example, all right angles are equal to one another.

The fifth of Euclid’s five postulates was the parallel postulate. The parallel postulate proved to be a source of puzzlement, irritation, and joy for mathematicians for millennia. The joy was usually short-lived, belonging to mathematicians who thought they had proven the postulate only to be disappointed when an error was identified in their ‘proof.’

Euclid had considered a straight line crossing two other straight lines. He looked at the situation when the interior angles (shown in the image below) add to less than 180 degrees. In these circumstances, he said that the two straight lines will eventually meet on the side of the two angles that add to less than 180 degrees.

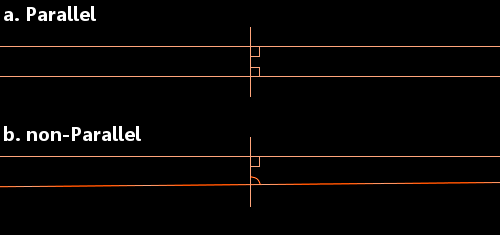
a. When each angle is 90 degrees, the lines are parallel.
b. If one or both of the angles is less than 90 degrees, the lines will meet.

Since the time Elements was first published, mathematicians had been trying to use Euclid’s first four postulates to prove the parallel postulate. They were doomed to fail. We now know that it is impossible to prove the parallel postulate using Euclid’s other postulates.

Omar Khayyam’s attempt was interesting. In his Explanations of the Difficulties in the Postulates in Euclid’s Elements he asks his readers to consider a straight line AB:

He asks his readers to consider two equal lines that are perpendicular to AB and sees three possible arrangements, which can produce four-sided figures:

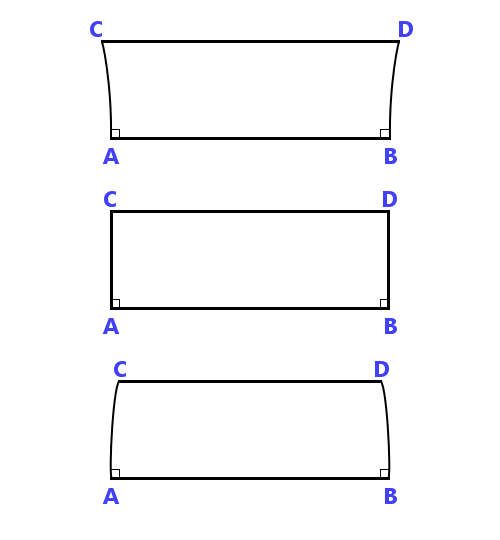
He then refutes the possibility that angles C and/or D can be anything other than right-angles and in the image above only the central option is possible. So, he believes he has proven the parallel postulate. In fact, he has not done so, all he has done is stated it in a different way.

What is interesting to historians of mathematics is that in Khayyam’s ideas – shown roughly in the images above – they can see the first glimmers of non-Euclidean geometry.

Some Personal Details and the End

Full details of Khayyam’s personal life are not known. He is believed to have married and had at least one son and one daughter.

In 1092, Malik Shah and his vizier both died – the first probably by poisoning, the second by assassination. Khayyam went into hiding during the resulting power struggle. His survival depended on lying low. He had been Malik Shah’s personal physician and become his close personal friend – which had made him enemies – and Khayyam’s poetry suggests his behavior may not have been devoutly religious – and this had also made him enemies. Khayyam actually published no poetry in his lifetime. Some of his musings would potentially have endangered his life.

After the power struggle, it took about 20 years for Khayyam to be fully rehabilitated and for him to emerge again, at 64 years of age, in the company of powerful people. However, he refused to teach. One of his poems suggests why this might be:

The secrets which my book of love has bred,
Cannot be told for fear of loss of head;
Since none is fit to learn, or cares to know,
Tis better all my thoughts remain unsaid.

Omar Khayyam died at the age of 83 in his hometown of Nishapur on December 4, 1131. He was buried in a tomb whose location he had chosen in an orchard where blossom would fall twice a year.

Khayyam’s poetry was popularized in the 1800s by Edward FitzGerald’s translations in the Rubaiyat of Omar Khayyam. Khayyam became so admired in the West that in 1963 the Shah of Iran had his grave exhumed and Khayyam’s remains moved to a huge purpose-built mausoleum in Nishapur where tourists could pay homage to the great poet.

We shall end with one of Khayyam’s most famous and evocative quatrains:

A Book of Verses underneath the Bough,
A Jug of Wine, a Loaf of Bread—and Thou
Beside me singing in the Wilderness—
And Wilderness is Paradise enow.”